How To Draw Position Velocity And Acceleration Graphs
Motion graphs, as well known every bit kinematic curves, are a common way to diagram motion in physics. The three motion graphs a high schoolhouse physics educatee needs to know are:
- Position vs. time (x vs. t)
- Velocity vs. fourth dimension (5 vs. t)
- Acceleration vs. time (a vs. t)
Each of these graphs helps to tell the story of the motion of an object. Moreover, when the position, velocity and acceleration of an object are graphed over the the same fourth dimension interval, the shapes of each graph relate in a specific and predictable fashion.
Setting up Motion Graphs
The x-axis on all motion graphs is always time, measured in seconds. The axis is thus always labeled t(due south).
The y-axis on each graph is position in meters, labeled x(m); velocity in meters per second, labeled five(g/s); or acceleration in meters per second squared, labeled a(m/stwo)
Tips
-
Beware of the position axis label 10 (m) – the "10" stands for deportation, not "x-axis"!
Movement graphs are often (though certainly not always) sketched without graphing specific points, instead showing a general shape that describes the relative motion of an object.
Position-Time Graphs
The position of an object tin can be positive or negative, depending on the frame of reference. Whatever the diagram shows, the coordinate aeroplane must match.
Consider the instance of a child riding forth a straight line eastward and and so west on her bike. Call east the positive management and west the negative management.
Hither is a graph of her ride:
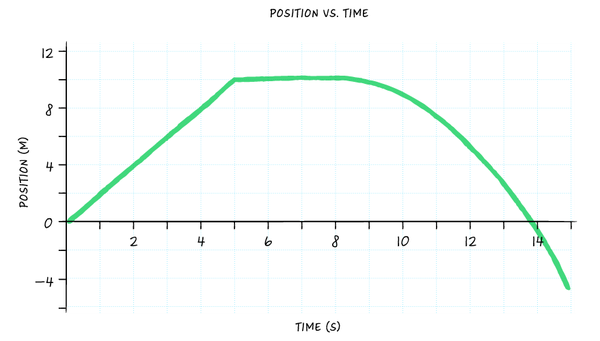
••• Dana Chen | Sciencing
For the first five seconds of her ride (from t = 0 to t = 5), she was moving at a constant rate to the east. This is indicated by the straight, increasing line in the positive quadrant of the position-fourth dimension graph. Some other mode to think of it is that her position is increasing positively.
In the next three seconds (t = 5 to t = 8), she stopped for a break. Her position does not alter in this time period, indicated by a abiding horizontal line stuck at +ten m.
Finally, the girl on the bike in the terminal part of her ride (t = 8 to t = 15) begins accelerating back in the westward management. This is indicated past a line that is not-constant (curved) and heading into the negative quadrant of the graph. The slope of the line increases over fourth dimension, in the negative direction, showing that her speed is increasing as she covers more ground every 2d.
Note that when she crosses the x-axis, she has passed by the identify where she started out.
Velocity-Time Graphs
Position-time graphs lead directly to velocity-time graphs: The slope of a position-time line shows the velocity of the object in the same time interval. This makes sense because position vs. time is just another way of saying meters per 2d – the definition of velocity.
In this case, the only deviation is what goes on the y-axis.
Consider the same daughter on her bike as in the final department. For the offset five seconds of her ride, she traveled 10 meters in 5 seconds, or 2 meters per second.
To graph her velocity in that same time interval and then, find 2 grand/s on the y-axis and draw a flat line for the first five seconds. Remember, her velocity didn't change, so the slope on this graph is naught. (Which means graphing her dispatch in this time interval should exist even easier – go along reading.)
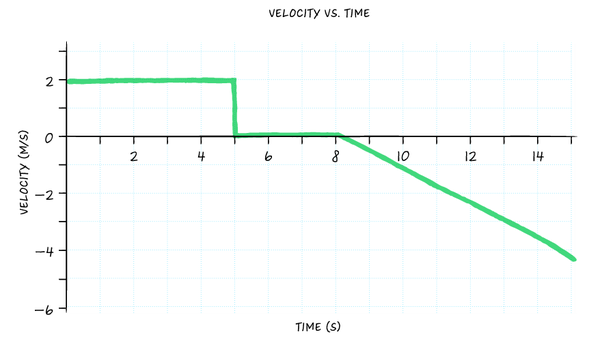
••• Dana Chen | Sciencing
And then, for the adjacent three seconds, she didn't motion at all, and so her velocity abruptly dropped to cipher. (Realistically, aye, she must have decelerated from 2 1000/s to 0 g/s in more than than an instant. But for the sake of simplicity hither, consider that her speed changed instantaneously.)
Of course, if her velocity is aught, that means there should be no curve on the graph over that time interval. In other words, the curve is now directly on meridian of the x-axis.
Finally, the girl started picking upward speed, backtracking homeward. Here the velocity graph gets interesting.
Assuming she had a constant acceleration – that is, each second she was increasing her velocity past the aforementioned amount as the 2nd before – this means her velocity was increasing at a constant rate. The twist in this scenario is that she likewise changed direction.
Tips
-
Think, a negative velocity does not hateful slowing down (that'due south negative dispatch). It means moving in the negative direction!
Altogether, that means the velocity-fourth dimension graph for the last segment of her ride (t = 8 to t = fifteen) needs to show a straight line where her velocity is growing negatively. In other words, a direct line moving from the 10-axis at t = 8 seconds in a diagonal towards the bottom right of the graph.
Acceleration-Time Graphs
These are frequently tricky for students; simply remember the meaning of acceleration: a modify in velocity.
For the beginning eight seconds of her ride, the daughter's velocity was not irresolute. (Again, ignoring her instantaneous shift from 2 m/s to stopped.)
That means for the first 8 seconds her acceleration was zero.
Making the move graph for this, where the y-axis is now showing acceleration in g/s2, is therefore pretty unproblematic:
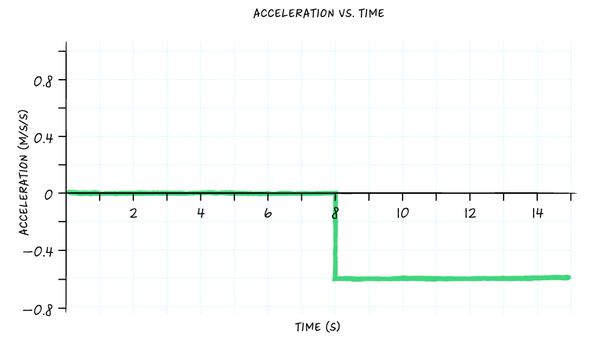
••• Dana Chen | Sciencing
Now, for the last portion of her ride, call up that her velocity was increasing at a abiding rate in the negative direction. Since increasing velocity is acceleration, the acceleration-time graph should have a flat line in the negative quadrant from eight seconds onward.
More Realistic Motility Maps
In the real globe, dispatch is oft not abiding. On the acceleration-time graph, this would look like a curved line.
Calculating the corresponding position-time and velocity-time graphs to become with this is typically beyond the telescopic of a not-calculus-based physics course. Students are expected to realize a curved line is not constant, still, and that the graph indicates a irresolute acceleration.
Tips
-
Examination yourself: How would you revise each of the previous graphs (position-fourth dimension, velocity-time and dispatch-time) to more realistically show the daughter'southward wheel slowing down before her intermission? Try it before reading on!
The graph for position should look roughly similar to what it did before, but with any abrupt corners smoothed out. The same would happen with the velocity graph - crude corners get smoothed out. But in addition, the instantaneous jump on the velocity graph from 2 grand/due south to 0 m/s becomes a smooth, slanted line with a large negative slope instead of a vertical line.
On the dispatch graph, at effectually the five second mark, a steep bend would dip into the negative region earlier coming back to 0 to bespeak the negative acceleration required to come to a stop. And the leap that occurs at the viii second marker, instead of being vertical, would but curve into a line with a large negative slope that then smoothly flattens out at -0.5 m/southward/s.
Source: https://sciencing.com/motion-graphs-position-velocity-acceleration-w-diagram-13720230.html
Posted by: hayesfille1954.blogspot.com


0 Response to "How To Draw Position Velocity And Acceleration Graphs"
Post a Comment